Fine-tuning Delete operation in AVL tree
The team of professor Fabinaris Suchbaum studies the standard AVL tree. They focus on tweaking the Delete operation.
Let X be a node in AVL tree. Let TL and TR be its left and right subtree, respectively. The procedure of deleting the node X is uniquely determined when TL or TR is empty. If both the subtrees are non-empty, there are two possibilities how to proceed (find either the largest key in TL, or the smallest key in TR,
and use it as a replacement for the key in X). The team members believe
that the optimal strategy of choosing the replacement should be based
on the average depths of nodes in TL (denoted as dL) and TR (denoted as dR), respectively. If dL ≥ dR then the replacement should be taken from TL, and if dL < dR then the replacement should be taken from TR.
The average depth dL (dR) is computed strictly with respect to TL (TR). The depth of a node in TL (TR) is its distance to the root of TL (TR).
Examples of choosing the replacement are given in Image 1 and Image 2.
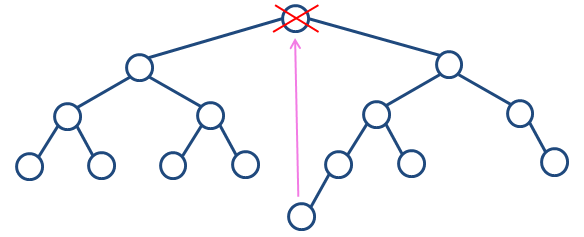 Image 1. Delete operation performed on the root. It holds dL=10/7 and dR=11/7, thus the replacement is taken from the right subtree. |
 Image 2. Delete operation performed on the root. It holds dL=34/15 and dR=26/12, thus the replacement is taken from the left subtree. |
The task
You are given a sequence of Insert and Delete
operations which are to be applied on an originally empty AVL tree. Each
Delete operation is implemented by the proposed strategy. For Delete
operations performed on nodes having both subtrees non-empty, calculate
the number of replacements taken form the left subtree as well as the
number of replacements taken from the right subtree.
For example, consider inserting keys 3, 2, 7, 1, 5, 8, 4, 6, 9 into an originally empty AVL tree and then performing delete(1). Both single and double rotations result in a balanced tree in this case. On the other hand, if we had to perform delete(6), delete(1) and apply double rotation then another unbalanced node (with key 7) would appear in the tree.
Input
The first input line contains integer N. Next, there are N lines, each specifying one operation. Operation Insert is specified by capital letter 'I' followed by space and an integer key. Operation Delete is specified by capital letter 'D'
followed by space and an integer key. There are no duplicate keys in
the input and also there are no Delete operations of non-existent keys. All key values are positive and less than 109.
It holds N ≤ 1.5×106.
Output
The output consists of one text line containing two non-negative integers L and R, separated by a space, where L is the number of Delete operations taking a replacement from the left subtree and R is the number of Delete operations taking a replacement from the right subtree.
Example 1
Input12 I 3333 I 2222 I 7777 I 1111 I 5555 I 8888 I 4444 I 6666 I 9999 D 6666 D 2222 D 7777Output 1 0 |
Insert 9999
3333____________
2222 ____7777
1111 5555 8888
4444 6666 9999
----------------------------------------
Delete 6666
3333________
2222 7777
1111 5555 8888
4444 9999
----------------------------------------
Delete 2222
________7777
3333____ 8888
1111 5555 9999
4444
----------------------------------------
Delete 7777
____5555
3333 8888
1111 4444 9999
----------------------------------------
Scheme 1. The tree in Example 1 in its final stages of developement.
|
Example 2
Input12 I 10 I 20 I 30 I 40 I 50 I 60 I 70 I 80 I 90 I 100 D 20 D 40Output 1 1 |
Insert 90
__40__
20 60__
10 30 50 80
70 90
------------------------------
Insert 100
__40______
20 __80
10 30 60 90
50 70 100
------------------------------
Delete 20
__40______
10 __80
30 60 90
50 70 100
------------------------------
Delete 40
__50____
10 __80
30 60 90
70 100
------------------------------
Scheme 2. The tree in Example 2 in its final stages of developement.
|
Example 3
Input37 I 21 I 13 I 29 I 8 I 18 I 26 I 32 I 5 I 11 I 16 I 19 I 24 I 27 I 31 I 33 I 3 I 6 I 10 I 12 I 15 I 17 I 20 I 23 I 25 I 28 I 30 I 2 I 4 I 7 I 9 I 14 I 22 I 1 D 33 D 26 D 21 D 13Output 0 3 |
Insert 1
______________21______________
_______13________ ____29____
__8___ __18 __26 32
_5 11 16 19 24 27 31 33
3 6 10 12 15 17 20 23 25 28 30
2 4 7 9 14 22
1
-------------------------------------------------------------
Delete 33
_______13______________
__8___ ____21________
_5 11 __18 __26____
3 6 10 12 16 19 24 __29__
2 4 7 9 15 17 20 23 25 27 31
1 14 22 28 30 32
-------------------------------------------------------------
Delete 26
_______13______________
__8___ ____21________
_5 11 __18 __27__
3 6 10 12 16 19 24 29__
2 4 7 9 15 17 20 23 25 28 31
1 14 22 30 32
-------------------------------------------------------------
Delete 21
_______13______________
__8___ ____22______
_5 11 __18 __27__
3 6 10 12 16 19 24 29__
2 4 7 9 15 17 20 23 25 28 31
1 14 30 32
-------------------------------------------------------------
Delete 13
_______14____________
__8___ ____22______
_5 11 __18 __27__
3 6 10 12 16 19 24 29__
2 4 7 9 15 17 20 23 25 28 31
1 30 32
-------------------------------------------------------------
Scheme 1. The tree in Example 3 in its final stages of developement.
|
Public data
The public data set is intended for easier debugging and approximate program correctness checking. The public data set is stored also in the upload system and each time a student submits a solution it is run on the public dataset and the program output to stdout and stderr is available to him/her.
Link to public data set