Experimental drone

A team of NASA scientists tests a special drone deployed on a distant planet. The drone is equipped with an experimental engine working on the principle of ionized gas compression and expansion. As the planet atmosphere is highly ionized, such an engine can be used. To simplify navigation of the drone, the scientists have divided the accessible area of the planet into sectors forming a regular rectangular grid. Each sector is assigned by a ionization level which is a non-negative integer characterizing the sector environment in average. The engine state is also characterized by its own ionization level. The drone can move only if this level is non-zero. Let the engine ionization level be E > 0 and let the drone be in a sector S1 of a ionization level I1. If the drone moves to a neighbouring sector S2 of a ionization level I2, the engine ionization level changes by the following rules (in the description we assume that Dmov and Denv are fixed positive integer constants such that 1 ≤ Dmov < Denv).
First, we calculate a change of the engine ionization level caused by the movement from S1 to S2.

Let E′ be the engine ionization level computed by the rules above. Second, we take E′ and calculate an additional change caused by the entered environment of sector S2. The obtained value is the engine ionization level in the entered sector S2. The scientists search for a minimum sequence of moves between neighbouring sectors which relocates the drone from the top-left sector to the bottom-right sector. Two sectors are neighbouring if they share a side.



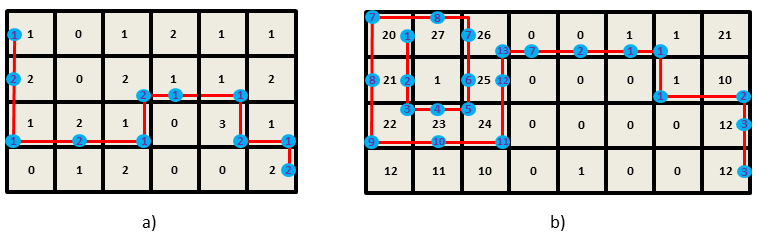
Image 1. Examples of sectors and optimal moves. Each black number in the middle of a sector is its ionization level. Optimal moves are represented by the red lines, blue ovals represent the drone in sectors during its relocation. The number inside an oval is the current engine ionization level. We assume for both examples that Dmov=1, Denv=5 and the initial engine ionization level is 1. The drone has to be relocated from the top-left sector to the bottom-right sector. a) The grid size is 4 × 6. The minimum number of moves required to reach the target sector is 10. b) The grid size is 4 × 8. The minimum number of moves required to reach the target sector is 22.

The task

Given an initial engine ionization level and a grid of sectors, find a minimum-length sequence of moves between pairs of neighbouring sectors that relocate the drone from the top-left sector to the bottom-right sector. Note that during such a movement the engine ionization level has to be non-zero, except for the moment the drone reaches the target sector (it is allowed to finish with engine ionization level equalling zero as the drone is not supposed to move anywhere further).

Input

The first input line contains integers M, N, Einit, Dmov, Denv separated by spaces. M is the number of grid rows, N is the number of grid columns, Einit is the initial engine ionization level, and Dmov, Denv are positive constants used by the rules defining the engine ionization level changes. Next, there are M lines, each of them containing N non-negative integers, separated by spaces, and determining ionization levels of sectors. Among these integers, the top-left sector is represented by the first integer on the first line, while the bottom-right sector is represented by the last integer on the last line.
Let Imax be the maximum value of all the input sectors ionization levels. It holds 2 ≤ M, 2 ≤ N, 1 ≤ Einit ≤ Imax ≤ 100, 1 ≤ Dmov < Denv, and M×N×Imax ≤ 8 × 106.

Output

The output consists of one line containing an integer which equals the minimum number of moves between neighbouring sectors required to relocate the drone with the initial engine ionization level Einit from the top-left sector to the bottom-right sector. It is guaranteed that a solution exists.

Example 1

Input
4 6 1 1 5
1 0 1 2 1 1
2 0 2 1 1 2
1 2 1 0 3 1
0 1 2 0 0 2
Output
10

Example 2

Input
4 8 1 1 5
20 27 26  0  0  1  1 21
21  1 25  0  0  0  1 10
22 23 24  0  0  0  0 12
12 11 10  0  1  0  0 12
Output
22

Example 3

Input
6 10 1 1 5
11 19 18 20  2  1  0 17  2  4
12 16 17  2  1  0 15 16 17 15
13 15  2  1  0  1 14 17 18  2
14  2  1  0 12 11 13 19  1  0
 2  1  0 13 14  4 15  2  0 15
 1  0 10 10 19  5  1  0  0 10
Output
48

The solution of Example 1 is visualized in Image 1a), the solution of Example 2 is visualized in Image 1b).

Public data

The public data set is intended for easier debugging and approximate program correctness checking. The public data set is stored also in the upload system and each time a student submits a solution it is run on the public dataset and the program output to stdout and stderr is available to him/her.
Link to public data set