Vystavené modely
Kvido je vášnivý modelář, který sestavuje RC modely letadel. Rád by si doma vystavil svoje výtvory nějakým originálním způsobem. Má plán, že v pokoji
připevní ke stropu tyč, na jejíchž koncích bude zavěšen buď model letadla a nebo připevněna jiná tyč, která bude podobným způsobem sloužit pro připevnění
dalších tyčí nebo zavěšení modelů. Celá instalace je demonstrovaná na Obrázku 1. V modelech má Kvido systém a přeje si, aby zleva doprava byly uspořádány
v předem stanoveném pořadí. Aby instalace měla stabilitu, pro každou tyč rozděluje Kvido modely na levou a pravou skupinu tak, aby absolutní hodnota
rozdílu mezi součtem hmotností modelů zavěšených vlevo a modelů zavěšených vpravo byla minimální. V případě více rovnocenných možností potom tak,
aby modely zavěšené na levou část tyče měly v součtu nejnižší možnou hmotnost. Toto pravidlo aplikuje Kvido nejprve na tyč zavěšenou ke stropu k rozdělení
všech modelů na levou a pravou skupinu, poté aplikuje pravidlo rekurzivně na následující tyče.
Po instalaci všech modelů si Kvido vzpomene, že má do letadel ještě dvě stejné figurky pilotů. Rád by je přidal do některých z letadel, přemýšlí
ale kam, aby stabilita zůstala co nejlepší.
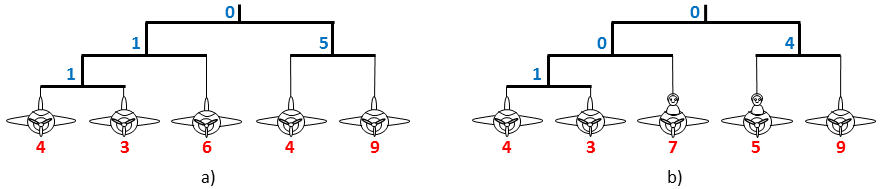
Obrázek 1. a) Příklad pěti zavěšených modelů letadel, které mají v pořadí zleva doprava hmotnosti 4, 3, 6, 4 a 9 (červená čísla pod obrázky letadel). Nejvýše umístěná tyč rozděluje modely na skupinu vlevo, jejíž celková hmotnost je 4+3+6=13 a skupinu vpravo s celkovou hmotností 4+9=13. Absolutní hodnota rozdílu hmotností obou skupin je 0 (modré číslo uprostřed tyče). Absolutní hodnoty rozdílů hmotností skupin jsou znázorněné i pro další tyče. b) Příklad optimálního přidání dvou figurek pilotů o hmotnosti 1. Jeden pilot je přidaný do třetího letadla, druhý do čtvrtého letadla. Hmotnosti letadel a nerovnováhy tyčí jsou přepočítané. |
Úloha
Je dána posloupnost celých nezáporných čísel M1, ..., Mk reprezentujících hmotnosti modelů, přičemž
Mi je hmotnost i-tého modelu. Proveďte rekonstrukci instalace ve tvaru binárního stromu T podle Kvidem stanovených pravidel.
To znamená, že každé i-té letadlo je umístěné v i-tém listu v pořadí inorder. Dále, absolutní hodnota rozdílu součtu hmotností letadel v levém a pravém
podstromu kořene je nejmenší možná, a zároveň v případě více rozdělení letadel s touto vlastností je vybraná ta možnost, která má součet hmotností letadel
v levém podstromu co nejmenší. Pravidlo je poté rekurzivně aplikováno na všechny vnitřní uzly stromu, v pořadí podle jejich vzdálenosti od kořene.
Definujme nerovnováhu vnitřního uzlu u stromu T jako absolutní hodnotu rozdílu mezi součtem hmotností všech letadel v levém podstromu uzlu u a součtem
hmotností všech letadel v pravém podstromu uzlu u. Spočítejte nerovnováhu celého stromu definovanou jako součet nerovnovah všech jeho vnitřních uzlů.
Rozhodněte, do kterých letadel v listech stromu T umístit figurky dvou pilotů tak, aby nerovnováha modifikovaného stromu byla nejmenší možná.
Umístění pilota do letadla zvyšuje hmotnost letadla o hmotnost pilota. Oba piloty je možné umístit do dvou různých letadel, ale také společně do libovolného
letadla (v tom případě je hmotnost tohoto letadla navýšena o dvojnásobek hmotnosti pilota).
Vstup
První řádek obsahuje dvě kladná celá čísla N a P, oddělená mezerou, kde N je počet modelů letadel a P je hmotnost figurky pilota.
Poté následuje druhý vstupní řádek, který obsahuje N celých kladných čísel oddělených mezerou. Tyto hodnoty reprezentují
hmotnosti modelů letadel a jsou dány v pořadí, které odpovídá systému uspořádání modelů zleva doprava.
Platí 2 ≤ N ≤ 1.5 × 106. Navíc, hmotnost každého letadla i pilota není větší než 7500.
Výstup
Na výstupu je jeden textový řádek s dvěma čísly oddělenými mezerou. První číslo je nerovnováha vytvořeného stromu T před přidáním pilotů, druhé číslo je nejmenší možná nerovnováha stromu T modifikovaného přidáním dvou pilotů. Je zaručeno, že ani jedno z těchto čísel není větší než 109.
Příklad 1
Vstup5 1 4 3 6 4 9
Výstup
7 5Data a řešení příkladu 1 jsou znázorněna na Obrázku 1.
Příklad 2
Vstup9 3 2 3 5 7 8 2 1 4 2
Výstup
11 9
Příklad 3
Vstup14 5 5 1 6 7 6 4 6 5 3 4 4 2 2 2
Výstup
23 26
Veřejná data
Veřejná data k úloze jsou k dispozici. Veřejná data jsou uložena také v odevzdávacím systému a při
každém odevzdání/spuštění úlohy dostává řešitel kompletní výstup na stdout a stderr ze svého programu
pro každý soubor veřejných dat.
Veřejná data