Minimum spanning tree in a graph with vertex potentials

Let G = (V, E, φ) be an undirected connected graph with the set of vertices V, set of edges E and a vertex potential function φ : V → ℕ0, assigning to each vertex u ∈ V a potential φ(u), which is a non-negative integer. For two vertices u, v of V, let d(u,v) denote their distance defined as the minimum length of a path from u to v where the length of a path is the number of its edges (note that d(u,u)=0 for each vertex u). Assume there is at least one vertex u' ∈ V such that φ(u') > 0. Define dmin(u) as the minimum distance from u to a vertex v with a nonzero potential, i.e. Define Dmin(u) as the set of vertices with nonzero potentials that are closest to u, i.e. Finally, define Φ(u) as the minimum potential of a vertex from Dmin(u), i.e. Based on the introduced functions, for each edge e = {u,v} ∈ E, define its weight wφ(e) as



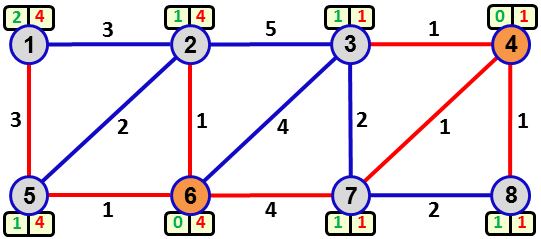
Figure 1. An example of a graph with the set of vertices {1,2,3,4,5,6,7,8} and 13 edges. There are two vertices (4 and 6) with nonzero potentials highlighted in orange, and it holds φ(4)=1 and φ(6)=4. The green number attached to a vertex u equals dmin(u), while the red number equals Φ(u). These numbers determine edge weights (the black numbers assigned to edges). For example, w({2,3}) = dmin(2)+dmin(3)+|Φ(2) − Φ(3)| = 1+1+|4−1| = 5. The red edges show a minimum spanning tree with respect to the calculated weights.

The task

Given an undirected connected graph G = (V, E, φ) with vertex potentials such that there are no two vertices u ≠ v with the same nonzero potential (i.e., u ≠ v, φ(u) > 0 and φ(v) > 0 implies φ(u) ≠ φ(v)), and the number of vertices with nonzero potentials is at least 1 and at most 1+ √ |V| , find a minimum spanning tree of the weighted graph G = (V, E, wφ).

Input

All the input graphs are of the form G = (V, E ∪ F, φ) where (V, E) is a grid with 4-neighbourhood system and F is a set of extra edges such that F ∩ E = ∅. Assume the grid consists of R ≥ 2 rows and C ≥ 2 columns. Then, the set of vertices V consists of all pairs (r, c) where r=1,...,R and c=1,...,C. Let (r, c) ∈ V. If r > 1, then E contains an edge connecting (r, c) and (r−1, c). If r < R, then E contains {(r, c), (r+1, c)}. If c > 1, then E contains {(r, c), (r, c−1)}. Finally, if c < C, then E contains {(r, c), (r, c+1)}. In addition, for each vertex (r, c) ∈ V, the set of extra edges can contain at most one edge connecting (r, c) with a vertex which is not its grid neighbour.

The first input line contains four integers R, C, P and K, separated by spaces. R is the number of grid rows, C is the number of grid columns, P is the number of vertices with nonzero potentials, and K = |F| is the number of extra edges. P input lines representing the nonzero potentials follow. Each of these input lines contains three integers r, c and p, separated by spaces. The integers determine that vertex (r, c) is of potential p. Finally, there are K input lines representing the extra non-grid edges. Each of these lines contains four integers r1, c1, r2 and c2, separated by spaces, and representing an edge {(r1, c1), (r2, c2)}.
It holds R*C ≤ 4*105, 1 ≤ P ≤ 1+ √ R*C  and K ≤ 2000. In addition, each vertex potential is not greater than 104.

Output

The output contains one line with one integer which equals the weight of a minimum spanning tree of G = (V, E ∪ F, wφ) where (V, E ∪ F, φ) is the input graph.

Example 1

Input
2 2 2 0
1 2 4
2 1 5
Output
4

Example 2

Input
2 4 2 3
1 4 1
2 2 4
1 2 2 1
1 3 2 2
1 4 2 3
Output
12

Example 3

Input
3 4 3 2
2 1 8
2 2 4
3 3 7
3 4 3 2
3 3 2 4
Output
21

The data and solution of Example 2 is isomorphic with the example in Figure 1.

Public data

The public data set is intended for easier debugging and approximate program correctness checking. The public data set is stored also in the upload system and each time a student submits a solution it is run on the public dataset and the program output to stdout and stderr is available to him/her.
Link to public data set