Smugglers vs Detectives

The detectives from law enforcement company Catch&Jail Ltd. investigate a group of smugglers. The detectives compiled an investigation list of these individuals. Before they crack down on the suspects they want to extract as much knowledge as possible from the information already available to the company.
A new criminal syndicate operates in the area and their people are organized into so called packs. The detectives are sure there are members of two packs in their list of suspects.

The following information is known to the detectives.

• Any two members of the syndicate are either connected or not. The pair of members who are connected communicate regularly and know each other, the pair who is not connected does not communicate, and the two individuals do not meet each other at all.
  
• The structure of all packs is identical, in the sense described below.
  
• No person can be a member of two or more packs.
  
• A pack is connected. It means that some members of the pack might not be connected, however there is a always a sequence of connections which leads from a member of the pack to any other member of the same pack. A sequence of connections is a sequence of persons P1, P2 P3, P4, ..., etc, such that there is a connection between P1 and P2, a connection between P2 and P3, between P3 and P4 etc. There can be even more than one sequence of connections between two members of a pack.
  
• All connections between the pairs of individuals in the detectives' list.
  
• The number P of members of a pack and the number C of all connections between the members of a pack.

• For any two different positions, say p₁ and p₂ in the first list, it holds
  the pair of members of the first pack at positions p₁ and p₂ are connected if and only if the pair of members of the second pack at the same positions in the other list is connected too.

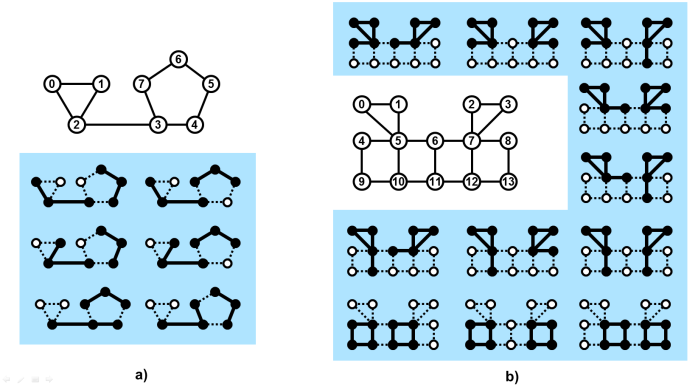
Figure 1. Schemes of connections between pairs of suspects in the investigation list. In case a), the list contains 8 individuals with 9 connections between some of them. In case b), the list contains 14 individuals with 19 connections between some of them. The smaller highlighted schemes, in each of the cases, present all possible pairs of packs in the given list. The members of the packs are shown as black dots and the connections between them are shown as thick lines. The values of P and C, respectively, are 3 and 2 in case a) and 4 and 4 in case b). The schemes correspond to Examples 1 and 2 below.

The task

You are given a list of all pairs of smugglers who are mutually connected. Also, you are given the size of the smugglers pack and the number of connections in a pack. Determine all possible pairs of packs in the given list.

Input

The first input line contains four positive integers N, M, P, C, where N is the number of smugglers in the list, M is the number of connections in the list, P is the pack size and C is the number of connections in a pack. For simplicity, the smugglers are labeled 0, 1, 2, ..., N−1.
Next, there are M input lines, each line represents one connection between two smugglers. The connection is listed as a pair of integers separated by space, the integers represent the labels of the smugglers in the pair.
The list of connections and also each particular connection are given in arbitrary order.
The following limits hold: 4 ≤ N ≤ 30, N−1 ≤ M ≤ 100, 3 ≤ P ≤ 7, 2 ≤ C ≤ 10,

Output

The output contains one or more text lines. Each line contains a possible pair of packs in the investigation list.
The pack which contains the member with the lowest label is listed first on the line, the other pack follows. A list of a pack is a sequence of the labels of its members sorted in ascending order.
The values on a line are separated by spaces. The lines are sorted in ascending lexicographical order.
There is always at least one possible pair of packs in the investigation list. The number of possible pair of packs is at most 5000.

8 9 3 2
0 1
0 2
1 2
2 3 
3 4
4 5
5 6
6 7
7 3

0 2 3 4 5 6
0 2 3 5 6 7
1 2 3 4 5 6
1 2 3 5 6 7
2 3 4 5 6 7
2 3 7 4 5 6

14 19 4 4
0 1
0 5
1 5
2 3
2 7
3 7
4 5
5 6
6 7
7 8
9 10
10 11
11 12
12 13
4 9
5 10
6 11
7 12
8 13

0 1 4 5 2 3 6 7
0 1 4 5 2 3 7 8
0 1 4 5 2 3 7 12
0 1 5 6 2 3 7 8
0 1 5 6 2 3 7 12
0 1 5 10 2 3 6 7
0 1 5 10 2 3 7 8
0 1 5 10 2 3 7 12
4 5 9 10 6 7 11 12
4 5 9 10 7 8 12 13
5 6 10 11 7 8 12 13

6 15 3 3
0 1
0 2
0 3
0 4
0 5
1 2
1 3
1 4
1 5
2 3
2 4
2 5
3 4
3 5
4 5

0 1 2 3 4 5
0 1 3 2 4 5
0 1 4 2 3 5
0 1 5 2 3 4
0 2 3 1 4 5
0 2 4 1 3 5
0 2 5 1 3 4
0 3 4 1 2 5
0 3 5 1 2 4
0 4 5 1 2 3

Public data

The public data set is intended for easier debugging and approximate program correctness checking. The public data set is stored also in the upload system and each time a student submits a solution it is run on the public dataset and the program output to stdout and stderr is available to him/her.
Link to the public data set