Požární stanice
Radní moderního města zjistili, že je zapotřebí vystavět ve městě určitý daný počet N požárních stanic. Město má tvar pravoúhlé obdélníkové sítě, ulice vedou buď směrem severojižním nebo východozápadním. Každá z požárních stanic má stát na některé křižovatce, pro polohu stanic však existují určitá omezení. V každé ulici bude stát nejvýše jedna požární stanice. Předpokládá se, že křižovatka je součástí obou ulic, které se v ní protínají. Dále, stanice nesmí být příliš blízko jedna vedle druhé, platí proto omezení, že každé dvě stanice musí být navzájem vzdáleny alespoň D jednotek, což vždy odpovídá alespoň D−1 křižovatkám na nejkratší cestě mezi těmito stanicemi. Nakonec, radní chtějí celý projekt dokončit za minimální cenu. Náklady na zřízení požární stanice jsou na různých křižovatkách různé a jsou známy pro každou křižovatku.
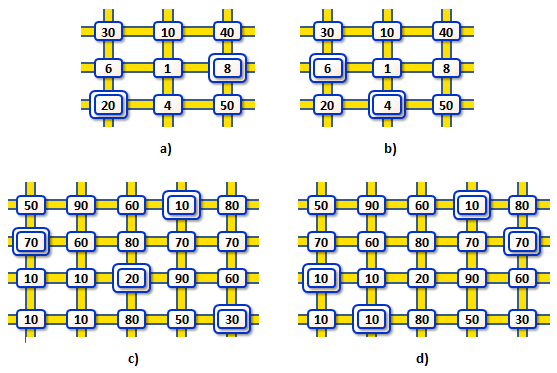 Obrázek 1. Schémata ulic ve městě s uvedenými náklady na výstavbu požární stanice na jednotlivých křižovatkách. Schémata postupně odpovídají příkladům 1 až 4 níže. Polohy stanic, které minimalizují stavební náklady a vyhovují podmínkám úlohy, jsou zvýrazněny. a) Dvě stanice, s minimální vzájemnou vzdáleností 3. b) Stejné město a stejné náklady jako v a), pouze minimální vzdálenost stanic je rovna 2. c) Čtyři stanice, s minimální vzájemnou vzdáleností 3. d) Stejné město a stejné náklady jako v c), pouze minimální vzdálenost stanic je rovna 2. |
Úloha
Je dán počet požárních stanic, které se mají vybudovat, jejich minimální možná vzdálenost a pro každou křižovatku náklady na vybudování požární stanice. Určete minimální náklady na vybudování daného počtu požárních stanic za předpokladu, že v každé ulici smí stát jen jedna stanice.
Vstup
První řádek obsahuje čtyři celá kladná čísla H, W, D a N oddělená mezerou představující po řadě počet východozápadních ulic, počet severojižních ulic, minimální možnou vzdálenost dvou požárních stanic a celkový počet požárních stanic, které se mají vybudovat. Následuje H řádků, každý představuje jednu východozápadní ulici. Na každém řádku je uvedeno W celých čísel oddělených mezerami, přičemž k-té číslo na r-tém řádku uvádí náklady na vybudování stanice na křižovatce r-té východozápadní ulice počítáno od severu a k-té severojižní ulice počítáno od západu.
Platí H×W ≤ 100, D, N ≤ 10, ostatní hodnoty nepřesáhnou 1000.
Výstup
Na výstupu je jeden textový řádek s jedním číslem udávajícím minimální náklady na vybudování N požárních stanic splňujících podmínky zadání.
Je zaručeno, že úloha má řešení ve všech předložených případech.
Příklad 1
Vstup3 3 3 2 30 10 40 6 1 8 20 4 50
Výstup
28Data a řešení příkladu 1 jsou znázorněna na obrázku 1a).
Příklad 2
Vstup3 3 2 2 30 10 40 6 1 8 20 4 50
Výstup
10Data a řešení příkladu 2 jsou znázorněna na obrázku 1b).
Příklad 3
Vstup4 5 3 4 50 90 60 10 80 70 60 80 70 70 10 10 20 90 60 10 10 80 50 30
Výstup
130Data a řešení příkladu 3 jsou znázorněna na obrázku 1c).
Příklad 4
Vstup4 5 2 4 50 90 60 10 80 70 60 80 70 70 10 10 20 90 60 10 10 80 50 30
Výstup
100Data a řešení příkladu 4 jsou znázorněna na obrázku 1d).
Veřejná data
Veřejná data k úloze jsou k dispozici. Veřejná data jsou uložena také v odevzdávacím systému a při
každém odevzdání/spuštění úlohy dostává řešitel kompletní výstup na stdout a stderr ze svého programu
pro každý soubor veřejných dat.
Veřejná data