Fixed Nodes (PY)

Each node in a undirected graph G is either black or white.
Let K and D be two non-negative integers. We say that a node x is (K, D)-fixed if there are exactly K black nodes in G which distance from x is exactly D. We remind you that the distance between two nodes a and b is equal to the minimum number of edges which must be traversed to get from a to b (or equivalently from b to a).

   

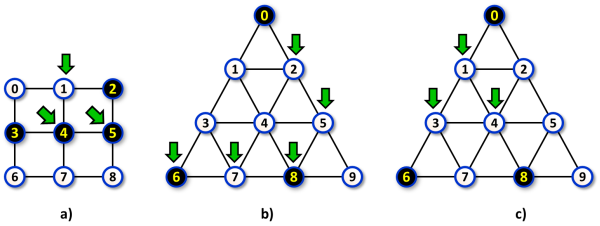Image 1. Graph sketches corresponding to Examples 1, 2, 3 below. The values of K and D are 2 and 1 in case a), 1 and 3 in case b) and 2 and 2 in case c). The (K, D)-fixed nodes are pointed to by green arrows.

The task

Count the number of (K, D)-fixed nodes in a given undirected graph.

---

Input

The first input line contains four integers N, M, K, D separated by space. The values M and N indicate (in this order) the number of nodes and the number of edges in the given graph. The nodes are labeled by integers 0, 1, ..., N−1.
Next, there is one text line which contains a list of all labels of black nodes in the graph. The list starts with an integer denoting the length of the list followed by node labels. All integers on the line are separated by spaces. The order of labels in the list is arbitrary. Next, there are M text lines, each describe one edge. Each line contains two integers A, B separated by space and representing the labels of the end nodes of the edge. The order of node labels on a line and the order of edges in the input is arbitrary.
It holds, 2 ≤ N ≤ 5000, 1 ≤ M ≤ 6000, 0 ≤ K ≤ N, 0 ≤ D ≤ N. The number of black nodes is at least 0 and at most N.

Output

The output contains one text line with one integer representing the number of (K, D)-fixed nodes in the given graph.

Example 1

Input

9 12 2 1
4 2 3 4 5
0 1
1 2
3 4
4 5
6 7
7 8
0 3
3 6
1 4
4 7
2 5
5 8

Output

3

The graph presented in Example 1 is depicted in Image 1a).

Example 2

Input

10 18 1 3
3 0 6 8
1 2
3 4
4 5
6 7
7 8
8 9
0 1
1 3
3 6
2 4
4 7
5 8
0 2
2 5
5 9
1 4
4 8
3 7

Output

5

The graph presented in Example 2 is depicted in Image 1b).

Example 3

Input

10 18 2 2
3 0 6 8
1 2
3 4
4 5
6 7
7 8
8 9
0 1
1 3
3 6
2 4
4 7
5 8
0 2
2 5
5 9
1 4
4 8
3 7

Output

3

The graph presented in Example 3 is depicted in Image 1c).

---

Public data

The public data set is intended for easier debugging and approximate program correctness checking. The public data set is stored also in the upload system and each time a student submits a solution it is run on the public dataset and the program output to stdout and stderr is available to him/her.
Link to public data set