Backup Connection
The buildings at Graphland Headquarters are interconnected by cutting edge quantum cables. There is a connection between any two buildings but not necessarily a direct one. Typically, a signal on its path from building A to building B may travel through other buildings too. At the beginning of the project, there was a list of pairs of buildings and each pair on the list was assigned a fixed value representing the cost of cable connection between those two buildings. When the projest was finished all buildings were connected using only some of the listed pairs and the total cost of all cables in the network was minimum possible.
Soon after the network completion it became obvious that the cheapest cable in the network is unreliable and its irreversible failure is only a matter of time. Loss of the cable would result in division of the network into two separate parts which would not be able to communicate. Therefore, a committee was assembled to deal with the threat. According to the committe, the solution to the problem is as follows: If the cheapest cable fails a substitution cable will be bought and installed. The substitution cable will run between one pair of the buildings which are on the original list and which are not directly connected now. The pair of buildings must be chosen in such way that the substitution cable will again connect the separate network parts and its price is neither too high nor too low. The definite upper and lower price limit was also set after lengthy consultations with the Headquarters Finance Department.
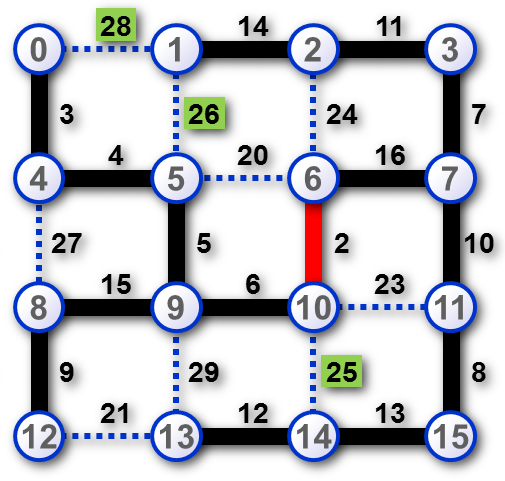 Image1. A schematic example of Headquarters buildings connection. The existing cables are depicted as bold lines, all other pairs of the buildings on the list are marked by dotted lines. The cheapest cable is depicted in red. The lower and the upper price limits for the substitution cable are 24 and 28, the candidate substitute connections are marked by prices highlighted in green. |
The task
You are given the list of possible connections between pairs of buidings and their prices. Also, you are given the lower and the upper price limit of the substitution cable. Create a list of all pairs of buildings which satisfy the conditions given by the committee.
Input
The first input line contains four positive integers N, M, C1, C2 separated by space. N represents number of buildings, M represents number of those pairs of buildings which can be directly connected by a cable, C1 and C2 represent the lower and the upper price limit for the substitution cable. We suppose that the buildings are labeled 0, 1, ... N−1.
The first line is followed by another M lines. Each of those lines contains three integers A, B, C separated by space. A and B are labels of buildings and C is the price for a cable connecting A and B directly.
The order of the pairs in the list is arbitrary. No pair of buildings appears in the list more than once.
No two cable prices in the list are the same.
Value of N does not exceed 2000, value of M does not exceed 1.5×106.
Output
The output contains more lines. The first line contains one integer representing the total price of the completed original Headquarters connection. This price is guaranteed to be positive and less than 109.
Next, there is one or more lines. Each of the lines contains labels of two buildings which may be connected by a substitution cable and the cable price. The values are separated by spaces and the smaller building label is written first.
The lines are sorted in increasing lexicographical order in which each integer is treated as a single symbol.
It is guaranteed that there is always at least one pair of buildings which satisfies the problem conditions.
Example 1
Input16 24 24 28 0 1 28 1 2 14 2 3 11 4 5 4 5 6 20 6 7 16 8 9 15 9 10 6 10 11 23 12 13 21 13 14 12 14 15 13 0 4 3 4 8 27 8 12 9 1 5 26 5 9 5 9 13 29 2 6 24 6 10 2 10 14 25 3 7 7 7 11 10 11 15 8Output
135 0 1 28 1 5 26 10 14 25The scheme corresponding to the Example 1 data is depicted in Image 1.
Example 2
Input8 13 8 11 0 1 11 1 4 10 4 7 6 7 6 8 6 3 9 3 0 7 0 2 12 2 5 1 5 7 13 1 2 2 2 3 4 4 5 3 5 6 5Output
28 1 4 10 3 6 9
Example 3
Input5 10 105 125 0 1 3 0 2 4 0 3 6 0 4 9 1 2 130 1 3 120 1 4 110 2 3 7 2 4 5 3 4 8Output
18 1 3 120 1 4 110
Public data
The public data set is intended for easier debugging and approximate program correctness checking. The public data set is stored also in the upload system and each time a student submits a solution it is run on the public dataset and the program output to stdout and stderr is available to him/her.
Link to public data set