Task: Counting Spanning Trees

Consider an undirected graph G consists of edges connecting vertices. A tree is a connected graph containing no cycles. A spanning tree is a subgraph of a graph that contains all its vertices and is itself a tree.

Your task is to count all different spanning trees for an input graph G. Two spanning trees are considered different if they differ in at least one edge.

The Input

The input contains description of the input graph G.

The first line consists of a single positive integer N (0 < N ≤ 1000) showing the number of vertices of the graph G.

The next lines contain a description of edges of the graph G in the following format: Every line is a couple of two integers separated by one space. Every integer is in range from 0 to N-1. These two integers represent one undirected edge in the graph G. We suppose that the vertices of the graph are labeled uniquely by integers 0, 1, ...,N-1.

The description of edges is terminated by the last line which has always two zeros separated by one space.

The Output

The output is always only one line with one nonnegative integer that represents the number of all spanning trees of the input graph.

You can assume that the output integer does not exceed 10^9.

Example 1:

Input:

4
3 0
3 1
3 2
0 1
1 2
2 0
0 0

Output:

16

Spanning trees:

The graphs below enumerate all spanning trees of the example above:

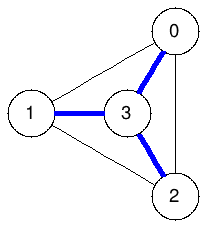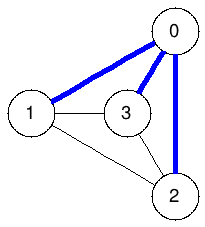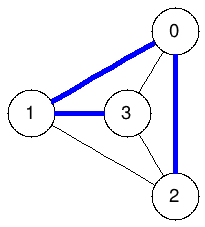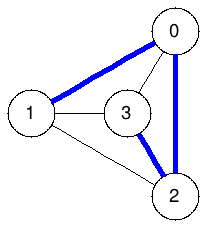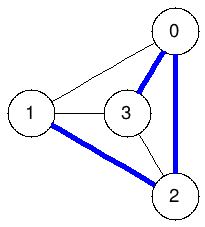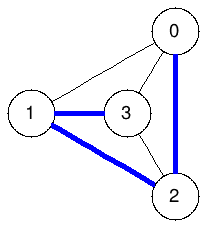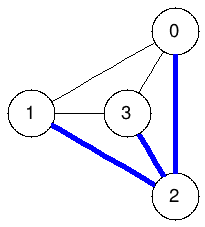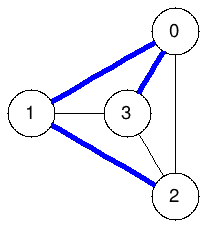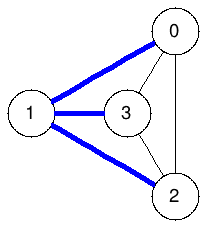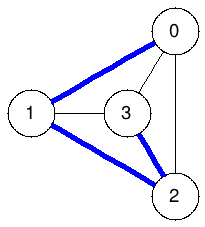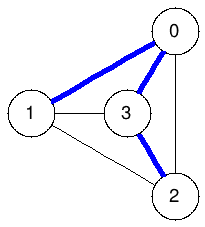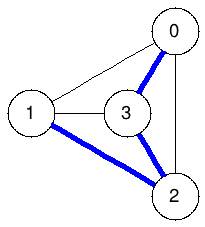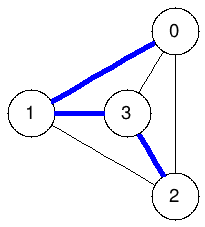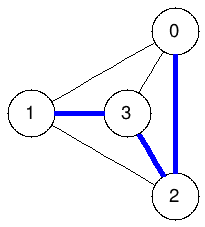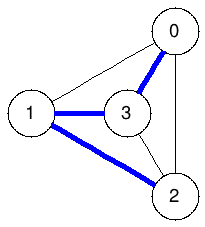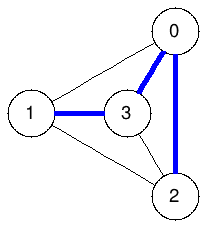Example 2:

Input:

5
0 1
1 2
2 3
3 0
4 0
4 1
0 0

Output:

11

Example 3:

Input:

10
0 1
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 0
0 0

Output:

10

Example 4:

Input:

16
0 1
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
10 11
11 12
12 13
13 14
14 0
15 0
15 1
15 2
15 3
15 4
15 5
15 6
15 7
15 8
15 9
15 10
15 11
15 12
15 13
15 14
0 0

Output:

1860496