Hedgehog minimum spanning tree
Let G be an unempty simple connected weighted graph. Let A be a non-empty subset of V(G). Let K be an integer for which holds1 ≤ K ≤ |A|.
We say that a subgraph S of G is (A, K)-hedgehog if there are at least K nodes in A which degree in S is 1.
The task
Your task is to find the minimum weight of all spanning trees of G which are (A, K)-hedgehogs. We remind you that the weight of a subgraph is the sum of all its edge weights.
Input
Input consists of more text lines. The first line contains number of nodes of graph G, the nodes are labeled 1, 2, ..., N.Next N lines contains weight matrix of G. Each input line contains one row of the weight matrix, each row is specified by N nonnegative integers separated by one or more spaces. We remind you that weight matrix is symmetric and its diagonal contains only zeroes.
The weight matrix is followed by line specifying the set A. First number on the line is the cardinality of A and it is followed by |A| distinct integers representing elements of A. All values are separated by one or more spaces.
Last line of the input contains value K. You may assume that 3 ≤ |V(G)| ≤ 99.
Output
Output consists of one text line which contains single integer value representing the minimum weight of all (A,K)-hedgehog spanning trees of G. If there are no (A,K)-hedgehog spanning trees in G, the output line contains value −1.Example 1
Input:6 0 3 0 1 0 0 3 0 3 0 1 0 0 3 0 0 0 1 1 0 0 0 9 0 0 1 0 9 0 6 0 0 1 0 6 0 4 1 2 3 6 2Output:
14
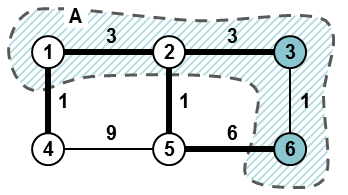
Fig. 1. Graph from example 1. Set A is highlighted, minimum ({1,2,3,6},2)-hedgehog spanning tree is drawn with bold edges, the two nodes in A, 3 and 6, which degree is 1 in the spanning tree are also highlighted. |
Example 2
Input:7 0 0 7 0 7 0 0 0 0 0 7 0 0 7 7 0 0 7 7 0 0 0 7 7 0 0 7 0 7 0 7 0 0 0 0 0 0 0 7 0 0 7 0 7 0 0 0 7 0 2 4 3 1Output:
-1
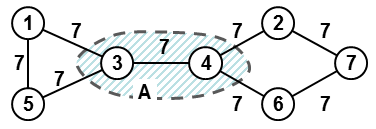
Fig. 2. Graph from example 2. Set A is highlighted. Any ({3,4},1)-hedgehog factor (= subgraph containing all nodes of the given graph) is necessarily disconnected due to the position of nodes 3 and 4 in the graph, therefore, there is no ({3,4},1)-hedgehog spanning tree in this graph. |
Example 3
Input:18 0 0 0 67 0 20 0 0 64 50 0 88 68 0 62 32 0 0 0 0 82 43 0 53 0 0 0 17 64 0 0 0 0 0 0 37 0 82 0 0 41 38 35 0 0 0 0 0 0 0 0 0 24 0 67 43 0 0 0 0 0 0 0 0 1 0 80 0 0 0 0 0 0 0 41 0 0 75 48 0 45 0 0 0 0 23 0 0 0 50 20 53 38 0 75 0 67 0 0 0 0 12 0 0 0 48 0 0 0 0 35 0 48 67 0 71 0 0 0 26 0 0 0 0 92 0 0 0 0 0 0 0 71 0 0 0 62 0 0 0 0 0 86 93 64 0 0 0 45 0 0 0 0 0 14 63 69 0 76 63 3 71 50 17 0 0 0 0 0 0 0 0 52 0 0 0 0 51 0 0 0 64 0 1 0 0 0 62 14 52 0 0 96 73 0 0 0 34 88 0 0 0 0 12 26 0 63 0 0 0 0 0 0 66 0 0 68 0 0 80 0 0 0 0 69 0 96 0 0 0 0 0 0 43 0 0 0 0 23 0 0 0 0 0 73 0 0 0 0 0 0 0 62 0 0 0 0 0 0 0 76 0 0 0 0 0 0 66 0 0 32 0 0 0 0 48 0 0 63 51 0 66 0 0 66 0 0 0 0 0 24 0 0 0 92 86 3 0 0 0 0 0 0 0 0 0 0 37 0 0 50 0 0 93 71 0 34 0 43 0 0 0 0 0 7 16 12 8 5 17 18 6 3Output:
498
Example 4
Input:25 0 1 0 51 0 0 20 59 35 17 94 46 14 92 0 0 64 95 34 78 84 41 26 23 7 1 0 0 12 23 0 15 51 67 63 63 0 76 0 0 71 60 72 0 97 0 43 92 23 38 0 0 0 19 64 62 86 5 0 13 19 0 70 73 89 96 80 43 26 3 69 76 25 0 70 51 12 19 0 50 0 10 0 31 99 0 44 97 88 0 52 57 64 0 65 0 71 32 95 48 0 23 64 50 0 48 0 0 24 0 43 0 15 0 83 0 0 0 83 65 72 19 99 26 31 0 0 62 0 48 0 64 56 0 51 5 0 0 90 60 0 99 0 0 0 99 0 0 6 50 20 15 86 10 0 64 0 93 29 17 61 4 42 32 42 0 0 0 6 31 63 9 0 33 41 59 51 5 0 0 56 93 0 0 71 34 0 47 43 74 55 88 0 17 0 38 0 37 29 87 35 67 0 31 24 0 29 0 0 81 0 11 58 51 0 95 0 0 32 3 24 30 73 66 83 17 63 13 99 0 51 17 71 81 0 82 24 27 0 0 30 18 0 0 48 89 43 32 43 77 94 63 19 0 43 5 61 34 0 82 0 20 33 0 0 99 69 0 81 56 0 57 65 34 0 46 0 0 44 0 0 4 0 11 24 20 0 33 0 0 0 0 15 1 56 92 91 98 30 29 14 76 70 97 15 0 42 47 58 27 33 33 0 4 0 35 0 57 89 18 94 66 35 53 0 92 0 73 88 0 90 32 43 51 0 0 0 4 0 42 99 18 55 0 34 66 62 55 98 0 0 0 89 0 83 60 42 74 0 0 0 0 0 42 0 0 75 95 30 0 19 0 93 61 34 0 71 96 52 0 0 0 55 95 30 99 0 35 99 0 0 0 45 40 46 50 38 68 59 46 64 60 80 57 0 99 0 88 0 18 69 0 0 18 75 0 0 54 8 64 53 78 52 28 41 95 72 43 64 0 0 0 0 0 0 0 15 57 55 95 45 54 0 12 29 99 26 38 0 35 34 0 26 0 83 0 6 17 32 0 81 1 89 0 30 40 8 12 0 57 85 0 45 0 65 78 97 3 65 65 0 31 0 3 48 56 56 18 34 0 46 64 29 57 0 73 0 0 29 68 84 0 69 0 72 99 63 38 24 89 0 92 94 66 19 50 53 99 85 73 0 53 72 20 0 41 43 76 71 19 0 9 0 30 43 57 91 66 62 0 38 78 26 0 0 53 0 67 86 30 26 92 25 32 99 0 0 37 73 32 65 98 35 55 93 68 52 38 45 0 72 67 0 55 0 23 23 0 95 26 6 33 29 66 43 34 30 53 98 61 59 28 0 0 29 20 86 55 0 93 7 38 70 48 31 50 41 87 83 77 0 29 0 0 34 46 41 35 65 68 0 30 0 93 0 20 8 7 18 3 6 20 16 5 24 9 22 15 19 25 2 1 12 13 4 21 4Output:
256
The public data set is intended for easier debugging and approximate program correctness checking. The public data set is stored also in the upload system and each time a student submits a solution it is run on the public dataset and the program output to stdout a stderr is available to him/her.