Identification of minimal DFA

Let us recall some necessary definitions. The concepts defined here are probably very well known to you, we provide the definitions just for the sake of completeness. A deterministic finite automaton (DFA) X is a five-tuple (A, S, S₀, δ, F) where

• A is an alphabet consisting of M ordered characters a₀ < a₁ < ... a_M-1, (1 ≤ M < ∞),
• S is an nonempty set of states,
• S₀ is a start state, S₀ ∈ S,
• δ is a transition function δ: S×A → S,
• F is an nonempty subset of S, it is a set of final states.

The Task

Let us consider two sets of words P and N. For these two sets holds that P ∩ N = ∅. Your task is to find a minimal positive integer number R, which represents number of states of some DFA Q that accepts all words in P and rejects (does not accept) all words in N. Furthermore, DFA Q allows to accept or reject any other word that is neither in P nor in N. The alphabet A of Q is induced by sets P and N, so any other character cannot be used in the definition of alphabet in Q.

Please note, that we do not know if this task can be solved in polynomial time (but we highly doubt it).

Input

The first line contains an integer number p that represents the size of set P.

Next p lines contain definition of the set P where every line represents a single word in P as a standard ASCII string.

The next line contains an integer number n that represents the size of set N.

Next n lines contain definition of the set N where every line represents a single word in N as a standard ASCII string.

Please note, that the alphabet A of Q is exactly defined by all used characters in the definitions of set P and N.

Output

Output contains only one line with the number R.

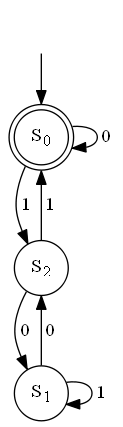
Example 1:

Input:

6
0
11
1001
10010
1100
10101
5
100
1
1000
111
101

Output:

3

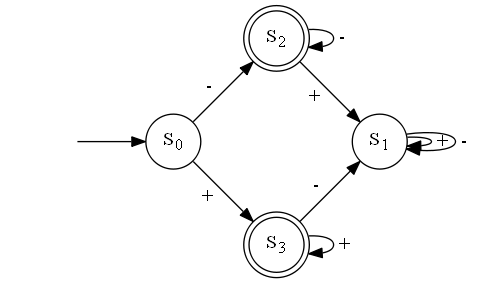
Example 2:

Input:

7
+
-
++
--
++++++++++
--------
+++
8
+-
-+
++-
-----++++++
-++
--+
+--
+---

Output:

4