Small Graphs Isomorphism

The score of an undirected simple graph (without self-loops) is a sequence of degrees of all its vertices sorted in non-increasing order.

The task
Find the number of all mutually non-isomorphic simple graphs with the given score.

Input

Input consists of one text line containing at least two integers. The first integer N specifies the number of vertices of the graph. Integer N is followed by N other integers specifying the score of the graph. All integers are separarted by space. Value N is at least 2 and at at most 12 and the sum of all values in the score is at least 2.

Output

Output consists of one text line containing one integer equal to the number of all mutually non-isomorphic simple graphs with the given score. Output value is greater than 0 and it does not exceed 100.

Example 1

Input:

6 3 3 2 2 2 2

Output:

4

   

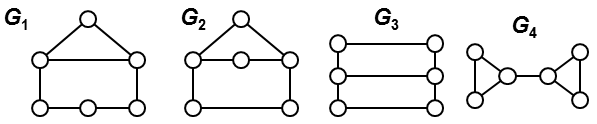Fig. 1. All four non-isomorphic graphs with score 3, 3, 2, 2, 2, 2.

Example 2

Input:

8 4 2 2 2 1 1 1 1

Output:

7

   

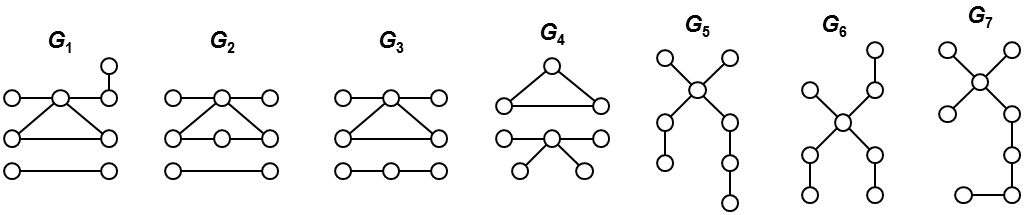Fig. 2. All seven non-isomorphic graphs with score 4, 2, 2, 2, 1, 1, 1, 1.

Example 3

Input:

12 4 4 3 3 2 2 0 0 0 0 0 0

Output:

5

   

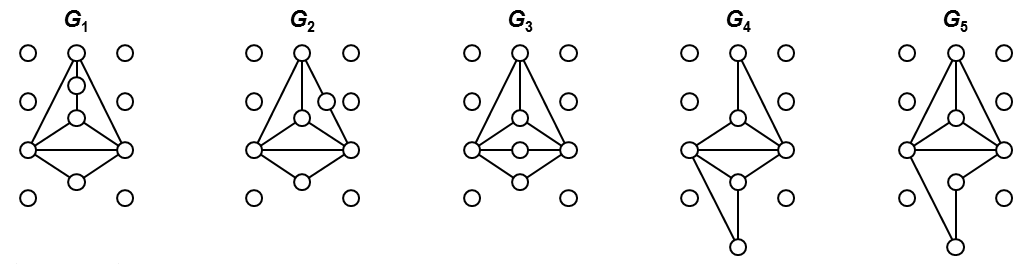Fig. 3. All five non-isomorphic graphs with score 4, 4, 3, 3, 2, 2, 0, 0, 0, 0, 0, 0.