Winter Maintenance Service
One unspecified road maintenance company is solving the following urgent task. Due to unexpected weather conditions - heavy snowfall in mid-winter, our unspecified company has only one winter service vehicle (snow plough truck) ready to use. Now it is necessary to remove snow from all serviced roads by that one vehicle. It is highly expected that the vehicle will remove all snow as quickly as possible so that it should not visit any road more than once. The serviced roads are defined by a number of crossings and by descriptions of directed connection between crossings. In other words, every lane between two crossings is defined by one description of directed connection between that crossings. Therefore, any serviced road between two crossings can be multilane. The winter service vehicle has to visit all lanes of serviced roads but a plough in front of the truck is able to operate only one lane at time. The start and the end crossing is not fixed, so the company can choose those locations on its own.
Your task is the following: How to schedule a tour for the winter service vehicle where the vehicle has to visit all lanes in the right direction and ordering only once?
Input:
The first line contains a number of crossings of all serviced roads. Next lines consist description of directed connections between crossings. Every line contains only one directed connection (one lane) represented by two integer numbers separated by space. The first number represents the start crossing and the second number represents the end crossing in some directed connection. Crossings are numbered from 0 to the number of crossings − 1. The last line of the input contains two zeros separated by space.Output:
If any solution does not exist then the output contains only one line with -1. A solution does not exist if the vehicle unable to visit each lane exactly once, no matter how the schedule is organized.
Otherwise, the output contains lines with directed connection with the same syntax format as the input. Moreover, it has to hold that an end crossing of any connection on output line n has to be the same as a start crossing on output line n+1. The first and the last crossing in the whole output are not, of course, covered by the previous restriction. The first line contains the number of crossings of all serviced roads as in the input. The last line of the output contains two zeros separated by space as in the input.
Any correct solution is accepted if the task can be solved in more ways than once.
Example:
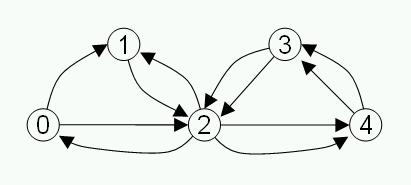
Input:
5 0 1 1 2 2 0 0 2 2 1 2 4 4 3 3 2 2 4 4 3 3 2 0 0
Output:
5 0 2 2 4 4 3 3 2 2 4 4 3 3 2 2 1 1 2 2 0 0 1 0 0