Marsh Causeway
The International Marshland Society is very interested in unique marsh habitats in tropical parts of Central America
which had only recently formed due to the quickly rising sea levels.
Biologists working in one such marsh had discovered and described some endemic plants with special
biochemistry properties which may stimulate fruitful genetic research in the future.
The plants tend to concentrate in small isolated areas or patches which typically measure
few decimeters across and which scientists call sites. To be able to monitor closely the
development of the sites the Society proposed to build a modern circular wooden causeway connecting
some of the sites, maybe all of them.
The causeway will consist of straight segments, each segment will connect two sites.
Each site connected by the causeway will be at the end of exactly two segments.
The causeway should not intersect itself, neither at a site nor at any other point.
For various environmental reasons, the length of the entire causeway should not exceed a given length limit D.
On the other hand, the couseway should connect as many sites as possible.
Among all possible causeways which length is less or equal to D and which connect maximum number of sites,
only those of minimum length should be considered and those are called optimal causeways.
The sites are of roughly equal importance, therefore there is no priority regarding which sites shoud be connected
if the length limit D prevents construction of a causeway connecting all sites.
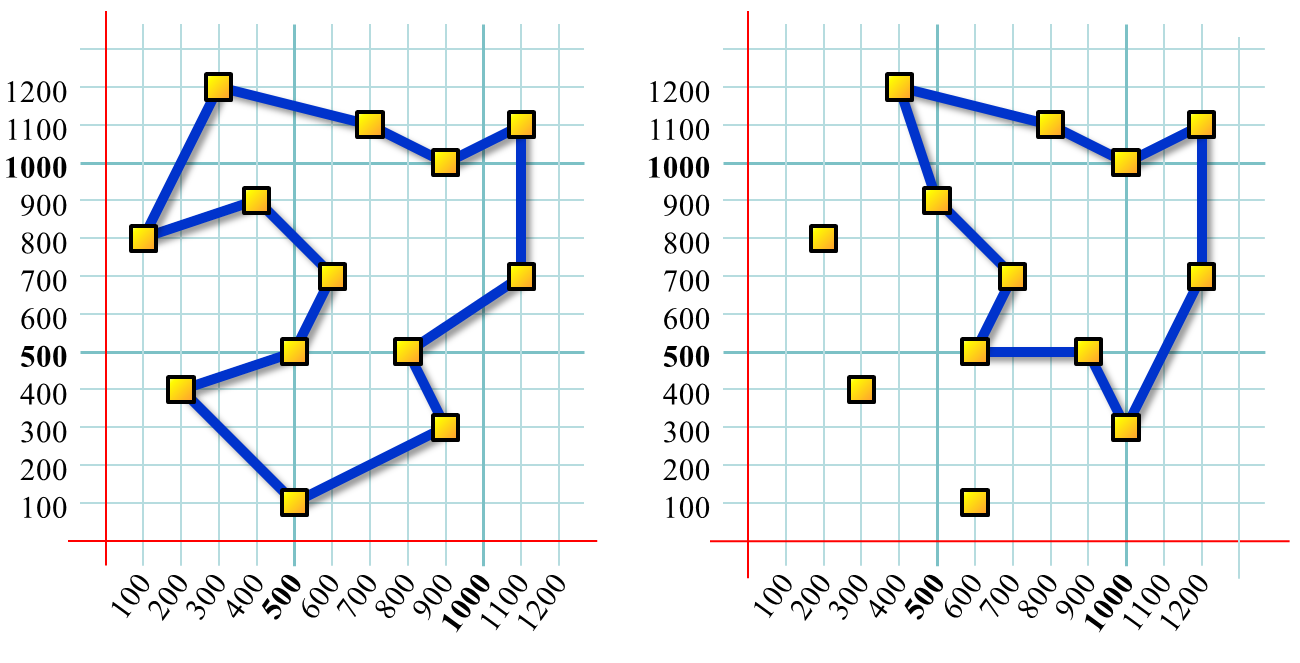 a) b) Image 1. Schemes of sites connected by the causeway projected on the rectangular grid. Scheme a) corresponds to Example 1, scheme b) corresponds to Example 2. In both cases the site locations are the same, the causeway length limit D is 4400 in case a) and 3400 in case b). The causeways depicted here are optimal in the sense described in the text. |
The task
You are given the coordinates of the botanical sites and the causeway length limit D. An optimal causeway C
satisfies conditions:
1. C connects maximum possible number of sites, it does not intersect itself and its length does not exceed D.
2. Length of C is minimal among all causeways which satisfy condition 1.
Find the length of an optimal connected causeway.
Input
The input contains several text lines. The first line contains two integer values N, D separated by space.
Value N is the total number of botanical sites in the marsh, D is the causeway length limit expressed in meters.
Next, there are N lines, each line specifies one site. The line contains two integers, separated by space, which
represent the x and y coordinates (in this order) of a site expressed in meters.
The order of sites in the input is arbitrary.
The value of N does not exceed 15, the value of D does not exceed 50000. All site coordinates are positive and less than 20000.
Output
The otuput contains single text line with one value representing the length in meters of the optimal causeway
rounded to the nearest bigger integer.
You may assume that the solution exists in all given problem instances.
Example 1
Input13 4400 100 800 200 400 300 1200 400 900 500 100 500 500 600 700 700 1100 800 500 900 300 900 1000 1100 700 1100 1100Output
4302The site locations and the causeway corresponding to Example 1 and its solution are depicted in the Image 1 a).
Example 2
Input13 3400 200 800 300 400 400 1200 500 900 600 100 600 500 700 700 800 1100 900 500 1000 300 1000 1000 1200 700 1200 1100Output
3054The site locations and the causeway corresponding to Example 2 and its solution are depicted in the Image 1 b).
Example 3
Input12 6000 100 100 1100 100 1100 1100 100 1100 600 200 700 500 1000 600 700 700 600 1000 500 700 200 600 500 500Output
5052
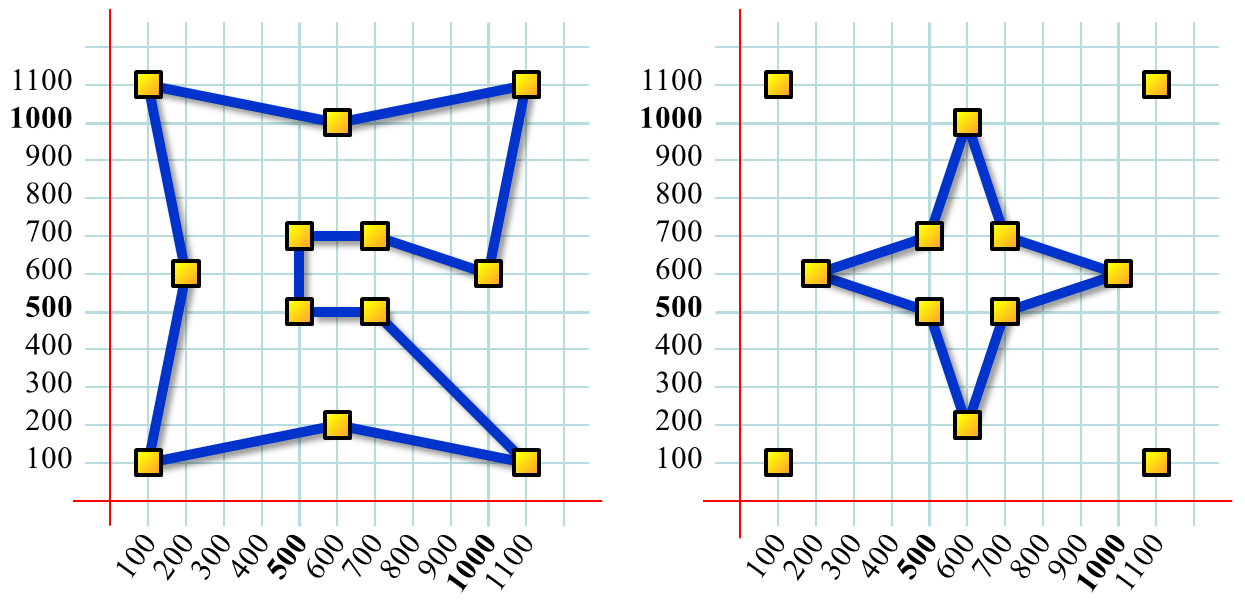 a) b) Image 2. Schemes of sites corresponding to a) Example 3 and b) Example 4. In both cases the site locations are the same, the causeway length limit D is 6000 in case a) and 3000 in case b). The causeways depicted here are optimal in the sense described in the text. |
Example 4
Input12 3000 100 100 1100 100 1100 1100 100 1100 600 200 700 500 1000 600 700 700 600 1000 500 700 200 600 500 500Output
2530
Public data
The public data set is intended for easier debugging and approximate program correctness checking. The public data set is stored also in the upload system and each time a student submits a solution it is run on the public dataset and the program output to stdout and stderr is available to him/her.
Link to public data set