New advances in gravitational waves observations

The Advanced Laser Interferometer Gravitational-Wave Observatory Two (ALIGO II) is undergoing a major overhaul. A calibration network connecting all wave detectors has to be built. Each connection between a pair of detectors is a costly item and therefore the network topology should not contain any cycles.
The cost of each connection is proportional to its length. The positions of all detectors are fixed. Thus, the cost of each possible connection between a pair of detectors is known in advance. If the length was the only ruling parameter then the obvious choice would be to build the network in the form of a minimum spanning tree of the graph which reflects all possible connections and their lengths. However, as one might expect, there are other issues to be taken into account in the project of this size. Theoretical calculations have indicated that the reliability of the system increases dramatically when some connections in the network share the same length. In fact, it has been shown that the noise interference in this specific kind of network falls off exponentially with the number of connections of the same length.
Considering the theory, the technical advisory board of the observatory has decided that the network building strategy should include three basic rules:

  1. The network has to be a tree.
  2. The network should contain maximum possible number of connections of some particular length, regardless of the cost associated with those connections.
  3. The total length of a network respecting the first and the second rule should be minimized.
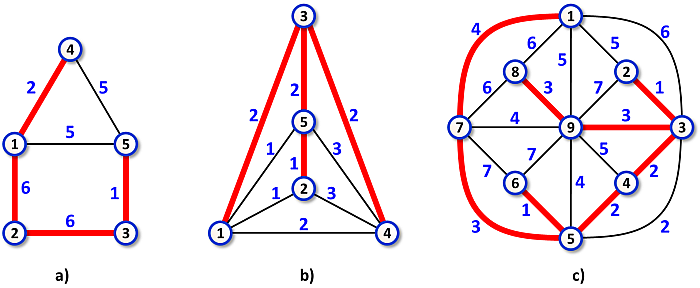
The total length of the network is equal to the sum of lengths of all connections in the network.

     


Image 1. Schemes of possible connections between pairs of detectors. The detectors are depicted as nodes, the possible connections are depicted as edges. The connections which may form the desired network are highlighted in red. The cases a), b), c) correspond to the Examples 1, 2, 3 below. Note that in some cases (e.g. in cases b and c) more than one network may satisfy the problem demands. However, all such networks share the same total length. Also note that the case a) illustrates the importance of rule 3. There exist spanning trees containing edges (1, 5) and (5, 4) which satisfy rule 2 but do not satisfy rule 3 as the total length of any of them is at least 17.

The task

You are given a list of all possible connections between the detectors and the respective connection lengths. Calculate the total length of a network which satisfies all three rules presented by the technical advisory board.

Input

The first line of the input consists of two integers N and M separated by space. Value N is the number of detectors. Value M is the number of possible connections between pairs of detectors. Next, there are M lines, where each line represents one possible connection. The line contains three integers D1, D2, L separated by space, meaning that the length of possible connection between detectors D1 and D2 is equal to L. The detectors are numbered from 1 to N. The possible connections are listed in a random order. It holds N ≤ 30000 and M ≤ 300000. Each length is at most 109.

Output

The output is one line containing the minimum total length of the required network. The result is not greater than 260.

Example 1

Input
5 6
1 2 6
2 3 6
5 3 1
5 4 5
1 5 5
4 1 2
Output
15
Example 1 input data and the resulting network are depicted in Image 1 a).

Example 2

Input
5 9
1 2 1
2 4 3
4 3 2
3 1 2
1 4 2
3 5 2
1 5 1
2 5 1
4 5 3
Output
7
Example 2 input data and the resulting network are depicted in Image 1 b).

Example 3

Input
9 20
1 2 5
2 3 1
3 4 2
4 5 2
5 6 1
6 7 7
7 8 6
8 1 6
9 1 5
9 2 7
9 3 3
9 4 5
9 5 4
9 6 7
9 7 4
9 8 3
7 1 4
1 3 6
3 5 2
5 7 3
Output
19
Example 3 input data and the resulting network are depicted in Image 1 c).

Public data

The public data set is intended for easier debugging and approximate program correctness checking. The public data set is stored also in the upload system and each time a student submits a solution it is run on the public dataset and the program output to stdout and stderr is available to him/her.
Link to public data set