Connected Networks

Computer network of the university campus consists of smaller local networks which are interconnected into one global network by backbone connections. There is one local network with tree topology in each building. Each local network contains a single master server. The backbone connections are installed among the master servers only. The system of backbone connections contains a loop running through all master servers and it also may contain some additional connections between those master servers which are not direct neighbours in the loop. (You may think of the backbone connections as a connected graph which contains a Hamiltonian circle.)
There are at most two types of local networks. Two local networks are of the same type if the graphs describing their topology are isomorphic and moreover there exists an isomorphism which maps one master server to the other one.
Examples of campus networks are depicted in Image 1.

     

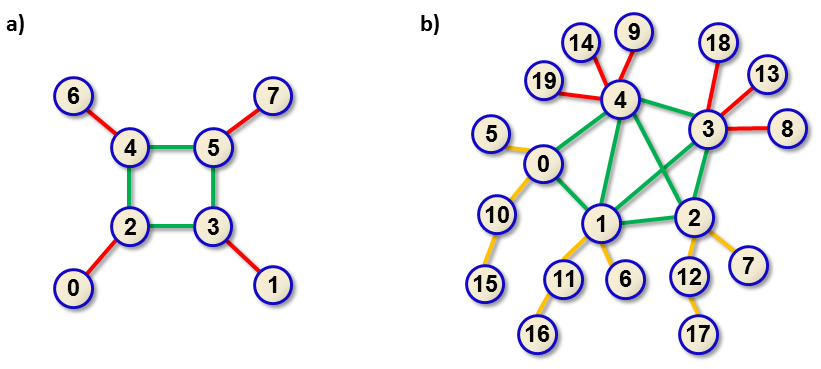
Image 1. a) Global campus network containing four local neworks all of which are of the same type. Master servers are nodes 2, 3, 4, 5, the backbone loop edges are depicted in green. Each local network consists of two nodes connected by a red edge. b) Global campus network containing five local neworks of two types. The first type occurs twice, the edges are depicted in red, master servers are 3 and 4. The second type occurs three times, the edges are depicted in orange, master servers are 0, 1, 2. The backbone connection is depicted in green, it contains loop 0 - 1 - 2 - 3 - 4 - 0 and three other connections.

The task

You are given a list of all direct connections between nodes in the global network. The information which connection belongs to the backbone and which connection belongs to a local network is lost. You have to reconstruct this information. In particular, you have to determine the number of local networks of each type.

---

Input

The first line contains two positive integers N, M separated by space and representing (in this order) the total number of nodes in the network and the total nuber of direct connections between two nodes. Next, there are M lines, each line describes one direct connection. The line contains two non-negative integers separated by space and representing the labels of one pair of two directly connected nodes. The network nodes are labeled 0, 1, ..., N−1. The connections are listed in arbitrary order.
Both values N, M do not exceed 520000. The distance from any node to the closest master server is at most 11.

Output

The output consists of one text line containing two non-negative integers X and Y separated by space. X denotes the number of local networks of one type and Y denotes the number of local networks of the other type. It holds that X ≤ Y. If the global network contains only one type of local network then X = 0.

Example 1

Input

8 8
6 4
5 7
5 4
4 2
2 3
3 5
0 2
3 1

Output

0 4

The network in Example 1 is depicted in Image 1a).

Example 2

Input

20 23
5 0
15 10
10 0
1 6
1 11
16 11
17 12
12 2
2 7
3 18
3 13
3 8
4 19
4 14
9 4
0 4
4 3
2 3
4 1
4 2
3 1
1 2
0 1

Output

2 3

The network in Example 2 is depicted in Image 1b).

---

Public data

The public data set is intended for easier debugging and approximate program correctness checking. The public data set is stored also in the upload system and each time a student submits a solution it is run on the public dataset and the program output to stdout and stderr is available to him/her.
Link to public data set