Words with given prefix
The task
There is a non-deterministic finite automaton A which accepts a finite language over an alphabet Σ. There is also a word P∈Σ*. We want to know the minimum and the maximum possible length of a word accepted by A which contains P as a prefix.
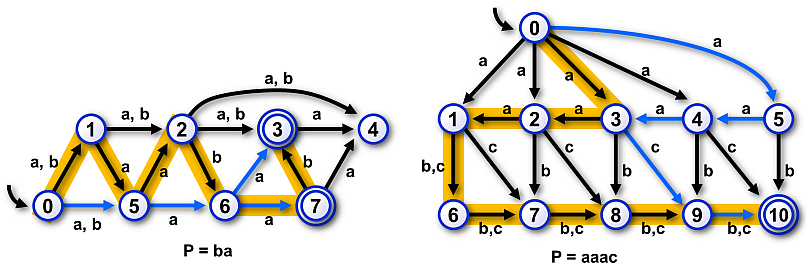
Image 1. Example 1 (left) and Example 2 (right). Transitions corresponding to selected accepted words with given prefix P and with minimum resp. maximum lengths are depicted by blue edges resp. black edges on highlighted background. |
Input
The first line contains two positive integers N, S separated by space and representing (in this order) the number of states in automaton A and the size of Σ. We suppose that the states of A are labeled 0, 1, ..., N−1.
Next, there are N lines specifying the automaton transition table. Each line represents one state.
A line starts with the label of the state and a mark which says whether the state is final or not. The mark is either '−' (minus sign) or 'F', final states are marked by 'F', all other states are marked by '−'. Next, the line contains all characters of Σ sorted in ascending order. Each character is followed by a list of states to which the automaton may transit from the current state after reading the corresponding character. The list is not sorted and might be empty. All values on a line are separated by one or more spaces.
The states of A are listed in ascending order of their labels, we suppose that the state labeled 0 is the start state of A.
The last line of input contains an unempty string P over Σ.
The size S of alphabet Σ is at most 26 and Σ consists of S consecutive lower characters of English alphabet 'a', 'b', ..., 'z', always starting from 'a'.
The value of N and the lenght of P both do not exceed 1000, automaton A is non-deterministic and the language it accepts is finite.
Output
The output consists of one text line containing two integers separated by space which denote (int his order) the minimum and the maximum possible length of a word over Σ which contains P as a prefix and is accepted by A.
Example 1
Input8 2 0 - a 1 5 b 1 5 1 - a 2 5 b 2 2 - a 3 4 b 3 4 6 3 F a 4 b 4 - a b 5 - a 2 6 b 6 - a 3 7 b 7 F a 4 b 3 ba
Output
3 6The automaton and the prefix P in Example 1 is depicted in Image 1 left.
Example 2
Input11 3 0 - a 1 2 3 4 5 b c 1 - a b 6 c 6 7 2 - a 1 b 7 c 8 3 - a 2 b 8 c 9 4 - a 3 b 9 c 10 5 - a 4 b 10 c 6 - a b 7 c 7 7 - a b 8 c 8 8 - a b 9 c 9 9 - a b 10 c 10 10 F a b c aaac
Output
5 8The automaton and the prefix P in Example 2 is depicted in Image 1 right.
Public data
The public data set is intended for easier debugging and approximate program correctness checking. The public data set is stored also in the upload system and each time a student submits a solution it is run on the public dataset and the program output to stdout and stderr is available to him/her.
Link to public data set