Historical Segmented Belts
The Archaeological department of the University of Outer Hebrides is currently investigating a collection of historical
ritual belts which were found at the various sites in this archaeologically rich area. Aside of their cultural significance
the belts also stand out due to their construction ingenuity and have been subject of intense study in recent years.
Each belt consists of some number of metal discs connected together to make a single wide loop.
Each disk is divided into radial segments of approximately same shape and area. The segments may (and they often do)
vary in their surface. A segment surface may be polished or rough, it may contain symbols or holes et cetera.
There is only a limited number of possible surfaces which makes expert classification of the belts somehow easier.
An intriguing property of a belt is that each disk can be freely rotated at its place in the belt.
The rotation is performed around the axis going through the center of the disk and perpendicular to its surface.
In addition, each disk can be flipped so that its back and front side are exchanged. The flipped disk retains its full capability to be rotated.
The surface of the front side and the back side of each segment
is the same, therefore the back side of the disk is the mirror image of the front side of the disk and vice versa.
To simplify the study and allow easier classification of the belts, each belt has been meticulously documented and described
by the procedure outlined in the next paragraph:
The belt is laid down on a flat table surface so that it has (approximately) circular shape. Then the researcher chooses one disk
and describes it. Next, he moves to one of the two immediately neighboring disks and describes that one. Then he moves to the next
neighboring disc in the same direction, describes it, and continues the process around the belt until the whole belt is described.
The description of a single disk is done in similar fashion. The researcher starts at any segment, writes
down the code of its surface and moves to one the two neighboring segments, writes down its surface code, moves to the next segment
in the same direction and so on.
The resulting description is a list of lists of segment codes, see also the example in the Image 1.
The description procedure is easy to follow but it has an obvious drawback. The description result depends on the original layout
of the disk on the table when it was being described. If the researcher chooses some other
layout he probably obtains a different description.
Two identical belts may therefore be described by two very different lists. On the other hand, the procedure is not easy to improve because
in any particular belt there are typically no prominent disks or segments or other features which would unambiguously
indicate in which place the description should start or in which direction should it progress or how the disks should be rotated or flipped.
Fortunately, at least the segment surface codes had been agreed upon before the first belt was described,
so they are unified in all descriptions.
The researches say that two belts are of the same type if they can be laid on the table side by side in such way that they
appear to be identical. Technically speaking, two belts are of same type if they can be laid on the table side by side in such way
that any particular description procedure applied simultaneously to both belts will produce two identical description lists.
The procedure is supposed to start at the same position on the both belts, proceed in the same direction and process the corresponding disks of
the two belts in the same order and the same direction. (Two disks are corresponding to each other if they are processed at the same moment in time.)
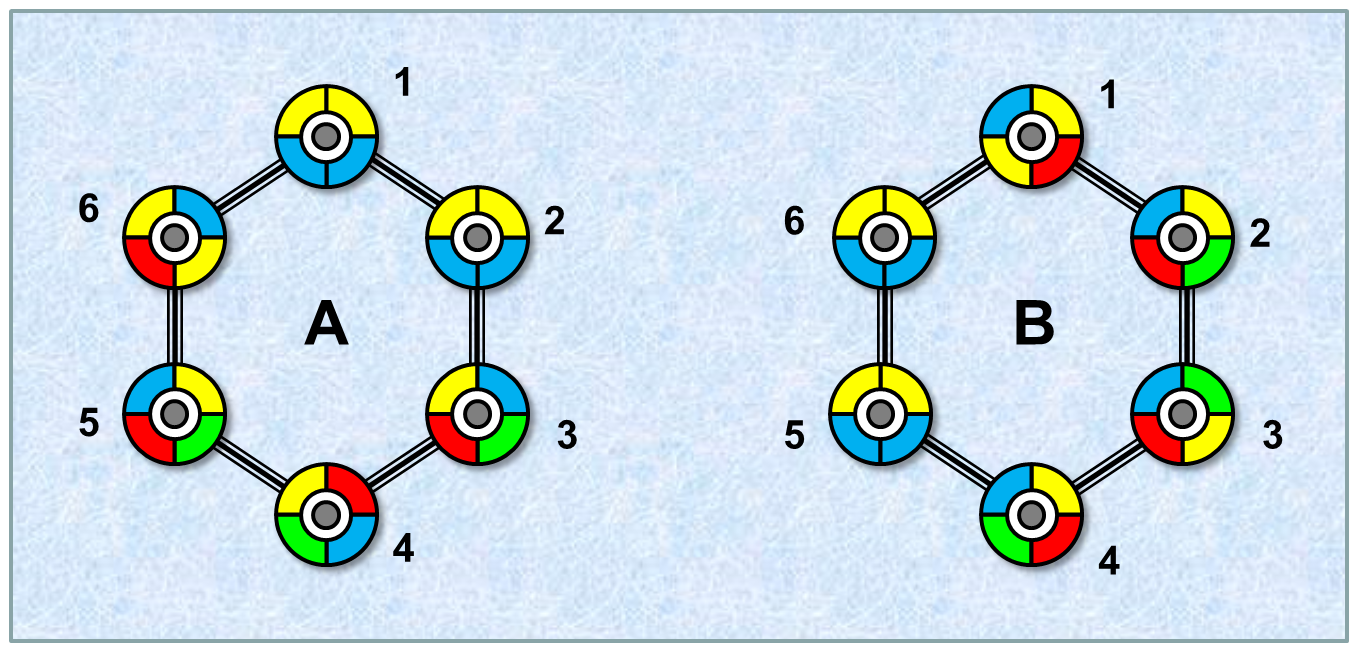 Image 1. Example of two belts and their possible descriptions. Each color represents one particular segment surface. Using color names abbreviations (b ... blue, g ... green, etc), belt A might be described by the list {ybby, bbyy, yrgb, yrbg, bygr, yryb}, belt B might be described by the list {yryb, bygr, rygb, rybg, bbyy, byyb}. To see that A and B are of the same type perform, for example, the following operations: Flip disk A4, flip disk A5, rotate belt A by 60 degrees clockwise, flip belt A along vertical axis, put it beside belt B and rotate each disk A1-A6 separately to obtain perfect visual match with belt B. After that, obviously, any description strategy applied simultaneously to both belts will produce the same description lists. |
The task
You are given the description of each belt in the collection. Determine how many different types of belts are there in the collection and divide the belts into separate groups according to their type.
Input
The input contains several text lines. The first line contains three integers N, D1, D2 separated by spaces.
N represents the number of belts in the collection, belts are uniquely labeled by integer values 0, 1, ..., N−1.
Value D1 represents the number of segments on each disk in each belt in the collection
and value D2 represents the number of disks in each belt in the collection.
Next, there are N lines, each contains a description of one belt.
The line contains belt label followed by space and D2 strings each of which has length D1. Neighboring strings are separated by single space.
Each string represents one disk of the belt, each segment of the disk is represented by one the 26 lowercase letters a,
b, c, ..., z according to the kind of its surface. Each kind of segment surface is represented consistently
by the same letter throughout the input. You may assume that each belt description was created by some instance of the description process
specified in the text above.
All values N, D1, D2 are positive and greater than 1. The value N does not exceed 1000, the value of D1×D2 does not exceed
1000.
Output
The output contains the partition of the collection into separate sets. Two belts belong to one set if and only
if they are of the same type.
The first output line contains the number of
sets, then each next line contains one set represented by the list of labels of all belts in that set.
The labels in the list are sorted in increasing order. The sets are sorted in non-increasing order
of their respective cardinalities. When two sets are of same cardinality then the set which list of labels is
lexicographically smaller occupies the line closer to the first output line. The labels in each list are separated by single space.
Example 1
Input3 4 6 0 ybby bbyy yrgb yrbg bygr yryb 1 yryb bygr rygb rybg bbyy byyb 2 yryb bgyr rgyb rybg bbyy byybOutput
2 0 1 2The first two belts of Example 1 are depicted in the Image 1.
Example 2
Input5 4 5 0 abba baab cbaa baac bbaa 1 baab aabb caab aabc bbaa 2 aabb aabb baac bbaa cbaa 3 abca abba baac baab bcaa 4 aabb bbaa caab bbaa aabcOutput
3 0 1 2 4 3
Example 3
Input3 9 3 0 rzyxwvuts aahgfedcb lkjiqponm 1 hgfedcbba mnopqijkl stuvwxyzr 2 fedcbaahg yzrstuvwx nopqijklmOutput
2 0 2 1
Example 4
Input24 2 4 0 ab bc cd de 1 ab bc de cd 2 ab cd bc de 3 ab cd de bc 4 ab de bc cd 5 ab de cd bc 6 bc ab cd de 7 bc ab de cd 8 bc cd ab de 9 bc cd de ab 10 bc de ab cd 11 bc de cd ab 12 cd ab bc de 13 cd ab de bc 14 cd bc ab de 15 cd bc de ab 16 cd de ab bc 17 cd de bc ab 18 de ab bc cd 19 de ab cd bc 20 de bc ab cd 21 de bc cd ab 22 de cd ab bc 23 de cd bc abOutput
3 0 5 7 9 14 16 18 23 1 3 6 11 12 17 20 22 2 4 8 10 13 15 19 21
Public data
The public data set is intended for easier debugging and approximate program correctness checking. The public data set is stored also in the upload system and each time a student submits a solution it is run on the public dataset and the program output to stdout and stderr is available to him/her.
Link to public data set