Trains dispatching
A dispatcher at a train station solves the problem how to optimally divide wagons into groups so that each group can be transported by a train to a warehouse. Each wagon is loaded by a cargo of some type. It is strictly prescribed how the wagon formation delivered to the warehouse by one train should look like (an ordered sequence of cargo types carried by each of the wagons is given). Wagons at the station are staying on one track. At each moment the dispatcher can only send away several first wagons by a train, keeping their order. This is repeated until all the wagons are dispatched. The wagons order at the station typically does not match the required formation order. Fortunately, the dispatcher does not need to fully comply with the formation requirement as it is possible to fix the formation on its way to the warehouse. There are small cargo supplies and cranes at some other stations which can either remove a wagon from the formation, insert a new wagon containing a cargo of any type to any position or to exchange the cargo of any wagon by a cargo of different type. However, for reasons of transport continuity, its possible to perform only a limited number of these changes per each train. The dispatcher is interested in two scenarios. The number of trains used to transport the wagons should either be the minimal possible (in order to save costs and ensure rapid transport) or maximal possible (to maximize the amount of cargo delivered to the warehouse).
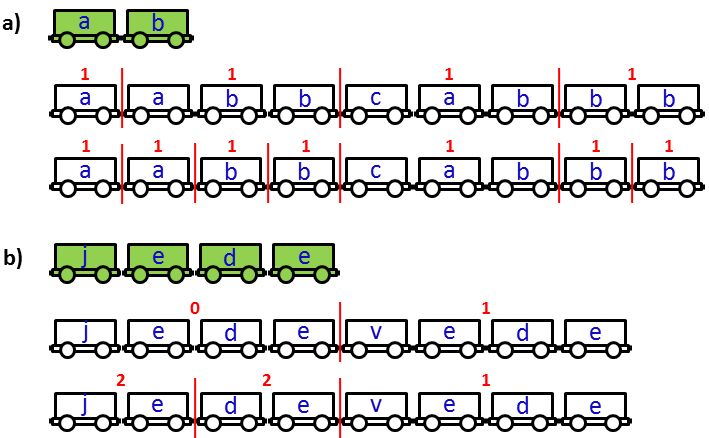
Figure 1. Examples of prescribed formations (green wagons) and wagons at the station divided (by red lines) into groups. Loaded cargo type is denoted by a lowercase letter. A division with the minimal number of groups is followed by a division with the maximal number of groups. The number of changes required to fix the formation is typed in red above each of the groups. The limit for the number of changes is 1 in case a) and 2 in case b). |
The task
Given a sequence of wagons with their cargo types at the station, a description of the required wagon formation and the number of changes that can be performed to a formation on its way to the warehouse, compute the minimal as well as maximal number of trains that can transport all the wagons.
Input
The first and second line of the input is a sequence of characters from the set {'a',..,'z'}.
The first sequence represents types of cargoes loaded to the wagons and it preserves the wagons order.
The second sequence is the formation of cargo types required by the warehouse.
The third line contains an integer C which is the maximal number of changes that can be performed to fix a formation on its way to the warehouse.
Let W be the number of wagons at the station and let F be the length of the required wagon formation.
It holds
W ≤ 7000, F ≤ 120, W × F ≤ 230000 and 1 ≤ C < F. It is always possible to transport the wagons by the given rules.
Output
The output is one line containing two integers separated by space where the first (second) integer is the minimal (maximal) number of trains that can transport the wagons to the warehouse.
Example 1
Inputaabbcabbb ab 1Output
4 7The data and solution of Example 1 are depicted in Figure 1 a).
Example 2
Inputjedevede jede 2Output
2 3The data and solution of Example 2 are depicted in Figure 1 b).
Example 3
Inputtntlsdtnttntlsdlsdtnt lstnnt 4Output
3 8
Public data
The public data set is intended for easier debugging and approximate program correctness checking. The public data set is stored also in the upload system and each time a student submits a solution it is run on the public dataset and the program output to stdout and stderr is available to him/her.
Link to public data set