Wayfarers
A group of wayfarers who call themselves "Children of the sun" plans to attend a festival in Sunshine city. To enjoy the journey there, they have decided to meet earlier at some place and to travel together through as many different cities as possible until reaching the destination city, even if this would require to visit some cities multiple times or to travel through identical routes several times. Note that only some cities are connected directly by a route. Moreover, for some routes, the wayfarers accept only one direction as they strictly refuse to travel with the sun behind. Examples are given in Image 1.
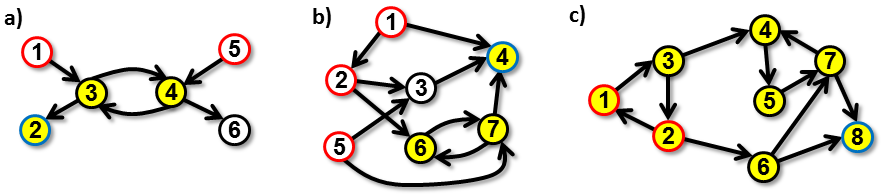
Figure 1. Examples of cities and acceptable direct routes among them. Hometowns of the wayfarers are circled in red, the destination city is circled in blue. The cities visited by an optimal route are highlighted in yellow. The optimal routes are e.g. as follows: a) the wayfarers meet in city 3, then they travel 3-4-3-2, b) meet in 7, travel 7-6-7-4, c) meet in 1, travel 1-3-2-6-7-4-5-7-8. |
The task
Given a list of cities, direct routes among cities acceptable by the wayfarers, hometowns of the wayfarers and the destination city, compute the maximal number of cities the wayfarers can visit together until finishing in the destination city (the destination city is counted as well).
Input
The first line of the input consists of four integers N, M, W, D separated by space.
Value N is the number of cities, M is the number of direct connections, W is the number of wayfarers and D is the destination city.
The next line contains W distinct integers which are numbers of hometowns of all wayfarers.
Next, there are M lines, where each line contains two integers A and B separated by space. This represents an acceptable route from city A to city B
(but not in the reversed order).
All the cities are numbered from 1 to N. Connections are listed in a random order.
It holds N ≤ 106, M ≤ 3 × 106 and W ≤ 1000. The destination city D can be reached by each wayfarer.
Output
The output is one line containing the number of cities the wayfarers visit together during an optimal route.
Example 1
Input6 6 2 2 1 5 1 3 3 2 3 4 4 3 5 4 4 6Output
3The data and solution of Example 1 are depicted in Figure 1 a).
Example 2
Input7 10 3 4 1 2 5 1 2 2 3 1 4 3 4 2 6 5 3 5 7 6 7 7 6 7 4Output
3The data and solution of Example 2 are depicted in Figure 1 b).
Example 3
Input8 11 2 8 1 2 1 3 3 2 2 1 3 4 4 5 7 4 5 7 7 8 6 7 6 8 2 6Output
8The data and solution of Example 3 are depicted in Figure 1 c).
Public data
The public data set is intended for easier debugging and approximate program correctness checking. The public data set is stored also in the upload system and each time a student submits a solution it is run on the public dataset and the program output to stdout and stderr is available to him/her.
Link to public data set